Cambiar la operación de cada cifra al moverla a un lado del igual e ir paso por paso hasta dejar a la X sola. Así puedes despejar la x en una ecuación sencilla.

Ejemplo de como despejar X en una Ecuación
- Tenemos esta ecuación : 2X + 3 = 13 X = 5
- Como el 3 esta sumando a 2X se pasa a restar al lado del 13 (2X = 13 – 3)
- Hacemos la resta (2x=10)
- Necesitamos dejar a la X sola, entonces pasamos el 2 que esta multiplicando a X, a dividir al 10 ( X = 10 / 2)
- De este modo el resultado será 5 que es el que nos da de la mencionada división

Trucos para que puedas aprender a despejar las incógnitas de una ecucación
Para ecuaciones sencillas como esta que hemos colocado arriba, lo cierto es que será raro equivocarnos, ya que tan sólo hemos de recordar como hemos de cambiar la operación de cada cifra al moverla a un lado del igual y que además tendremos que ir paso por paso hasta dejar a la X sola.

Otro truco, aunque yo no suelo fiarme mucho de este es la de utilizar solo números; me explico:
Si encuentras una fórmula X+B=C y quieres despejar la X por ejemplo, cambias las letras por numeros 5+4=9 así que si tienes que despejar seria 5=9-4 es decir X=C-B de este modo podemos aprender la base de como comenzar a despejar una ecuación ya que poco a poco nos daremos cuenta de que la cosas se irá complicando con más números y operaciones.
Por otro lado para aquellas que sean algo más complicadas, tenemos trucos como por ejemplo:
- Multiplicar o dividir por una constante distinta de cero ambos miembros de la ecuación
-
Multiplicar por un polinomio ambos miembros de la ecuación
Ejemplo: Si en la ecuación 2x=10, multiplicamos por ( x -1), nos queda la ecuación) 2x (x-1)= 10 (x-1) y cuyas soluciones son 5 y se agregó una solución.
Elevar al cuadrado ambos lados de una ecuación.
Ejemplo : Si en la ecuación 1=x , cuya solución es explícita, elevamos ambos miembros al cuadrado nos queda 1^2=x^2 , donde el lector puede verificar que sussoluciones son -1 y 1. De nuevo se agregaron soluciones.
Cómo resolver la ecuación x+a=b
Toda ecuación se resuelve a través de la transposición de términos. Cada vez que un elemento pasa de un lado a otro de la ecuación, el signo del elemento cambia.
Por ejemplo, si la ecuación es x+a=b y queremos despejar ‘x’, haríamos lo siguiente:
x+a=b
x=b-a
Pero si la ecuación fuese x-a=b el valor de ‘x’ cambiaría, aunque la forma de despejar ‘x’ sería la misma:
x-a=b
x=b+a
A continuación, vamos a poner un ejemplo en el que ‘a’ y ‘b’ son valores numéricos. Empecemos por la primera ecuación:
x+a=b
x+3=25
x=25-3
x=22
Ahora vamos a resolver la segunda ecuación, teniendo las incógnitas ‘a’ y ‘b’ otros valores diferentes:
x-a=b
x-7=10
x=10+7
x=17
Mira como resolver una ecuación x+y
Un sistema de ecuaciones con dos incógnitas se puede despejar siguiendo el método de eliminación. Lo importante para poder calcular el valor de cada incógnita es ir por partes: primero debemos eliminar una de las dos incógnitas para poder calcular el valor de la que quede. Una vez sepamos el valor de ‘x’, por ejemplo, podremos proceder a calcular el valor de ‘y’ sin mayores problemas. ¿No te ha quedado del todo claro? ¡Pues no te preocupes! A continuación, desarrollaremos el proceso para que puedas aprender a resolver una ecuación x+y.
Para ello, antes de nada, necesitamos una ecuación x+y:
x+6y=16
A continuación, eliminaremos la incógnita ‘y’ para después sumar la incógnita ‘x’ y los dos resultados de la ecuación:
x+6y=16
4x-6y=34
El procedimiento anterior y el cálculo del valor de la incógnita ‘x’ es el siguiente:
x+4x=5x; +6y-6y=y; 16+34=50
5x=50; x=50/5; x=10
Una vez tenemos el valor de ‘x’ procedemos a sustituirlo en la ecuación inicial y calcular el valor de ‘y’:
x+6y=16
10+6y=16
6y=16-10
6y=6
y=6/6
y=1
Y ahora podemos comprobar que ambos valores son correctos, es decir, si x=10 e y=1 la ecuación sin incógnitas sería:
10+6=16
Ecuaciones de primer grado para solucionar
Una ecuación existe porque algo (‘x’) es igual a algo. En este caso podríamos decir que una ecuación de primer grado sería una ecuación igual a otra ecuación. Otra cosa que caracteriza a este tipo de ecuaciones es que solo hay una incógnita: ‘x’.
A continuación, dejamos un ejemplo de ecuación de primer grado:
12+3x=20-x
Primero, pasa las ‘x’ a un lado de la ecuación mediante la transposición y los número al otro lado de la ecuación con el mismo procedimiento. La ecuación quedará de la siguiente manera:
3x+x=20-12
Ahora solo tienes que despejar ‘x’ y, a continuación, calcular el valor de la incógnita. El resultado sería el siguiente:
4x=8
x=8/4
x=2
¿Sabés resolver las ecuaciones de segundo grado?
Para calcular la solución de una ecuación de segundo grado completa se debe calcular la raíz de la misma. Se llama raíz a la solución que nos permitirá factorizar, en la medida de lo posible, la ecuación. Factorizar consiste en simplificar la ecuación y convertirla en una de primer grado.
Se utilizará para llegar a dicha solución la fórmula cuadrática en primer lugar:
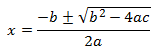
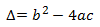
Y, en segundo lugar, debemos factorizar una ecuación de segundo grado de la siguiente manera:
x2+2x+1=(x+1)(x+1)
A y B en este caso deben considerarse como dos posibles soluciones a la ecuación:
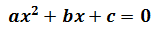
Si lo entendemos de esta manera, podemos factorizar la ecuación anterior, es decir, simplificarla así:
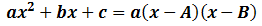
Si la única solución es A (con multiplicidad 2), podemos factorizar de la siguiente manera:
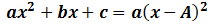
Avanzando un poco el nivel, pronto tendrás que saber resolver también ecuaciones de segundo grado. En este caso no hay truco, solo necesitarás tener unos conocimientos previos, por ejemplo saber hacer raíces cuadradas, y aprenderte una fórmula.
Esta fórmula es el único secreto y la base fundamental imprescindible para saber hacer ecuaciones de segundo grado. Hasta que no te sepas esta fórmula de memoria, nunca sabrás resolverlas.

Puede parecer una fórmula algo complicada al principio, pero verás que todas las operaciones que debes realizar son muy sencillas. Para entenderlo mejor, imagina que tienes una ecuación que es:
- x2 + 3x + 2 = 0
Lo que debes hacer es asignar a cada grupo numérico una de las letras (a, b y c) de la fórmula. Es muy sencillo.
- 4×2 sería la “a”.
- 3x sería la ”b”
- 2 sería la “c”
De esta manera puedes deducir perfectamente que:
- A = 4
- B= 3
- C = 2
Ahora que ya sabes estos datos, simplemente tienes que aplicarlos a la fórmula. De esta manera te quedaría.


Como ves, las ecuaciones de segundo grado tienen siempre dos soluciones. Recuerda siempre poner los signos + y – correctamente. En este caso todos los valores son positivos, pero imagínate que la ecuación fuese:
- x2 -3x + 2 = 0
En este caso, el valor de “b” sería -3, pero si te fijas, la fórmula empieza con “-b”, por tanto, pasaría con valor positivo. Es decir, la resolución de la ecuación sería la siguiente. Haz la prueba:

Lo único que tienes que hacer es fijarte y hacer bien las operaciones. Recuerda también que la raíz cuadrada solo abarca a los productos “b2-4ac”, mientras que la fracción debe hacerse sobre todo el numerador.
El último y mejor consejo que podemos darte es que te aprendas esta fórmula de memoria. Verás cómo en poco tiempo hacer estas ecuaciones será lo más fácil.
Esperamos que con estos consejos hayas aprendido a despejar la X en una ecuación, tanto en las ecuaciones de primer grado como en las ecuaciones de segundo grado (¡apréndete la fórmula ya!). Pero a medida que vayamos superando lecciones y pasando de cursos los problemas serán cada vez más complicados y, en el caso de despejar a X, nos encontraremos con operaciones con varias incógnitas, como es el caso de aquellas en las que tengamos que despejar x, y y z.
Estas son las ecuaciones de tercer grado
Igual que hemos podido comprobar que las ecuaciones de segundo grado tienen dos posibles soluciones, en el caso de las ecuaciones de tercer grado debemos tener en cuenta que habrá tres soluciones posibles.
Lo primero que comprobaremos es si se puede factorizar la ecuación:
ax3 + bx2+ cx + d = 0
Si se puede factorizar la ecuación, debemos factorizar la ‘x’:
x(3x2 + -2x + 14) = 0
Como puedes observar, nos quedaría una ecuación de segundo grado que podemos resolver con los mecanismos y procesos enumerados en la sección anterior.
También podemos identificar si la ecuación de tercer grado tiene una constante, es decir, si tiene un valor ‘d’. De no ser así, si la ecuación no es una constante, cabe destacar que podemos utilizar la fórmula cuadrática para resolver la parte de la ecuación que está entre paréntesis.
Por tanto, como has podido comprobar las ecuaciones de segundo grado tienen dos posibles soluciones y las ecuaciones de tercer grado tienen tres posibles soluciones. Si no te ha quedado del todo claro te recomendamos que eches un vistazo a otros ejemplos y navegues por Internet hasta encontrar un vídeo con ejercicios de ecuaciones. Ya verás como en muy poquito tiempo consigues convertirte en el mayor experto sobre ecuaciones. Ya se sabe que si algo te cuesta lo mejor que puedes hacer es practicar, practicar y practicar. La constancia siempre da sus frutos. ¡Ánimo con las matemáticas!
Aprende como despejar x, y, z en una ecuación
En este caso se denomina ecuación de Gauss al método que se utiliza para resolver una ecuación de este tipo. En este caso, tenemos ecuaciones de 3 incógnitas, del tipo 2x + 3y – 4z = 8. En este caso, el proceso para hallar el valor de x, y o z, es un poco más complejo y difícil de explicar mediante palabras. Es por ello que os dejamos un video muy interesante y didáctico en el que podéis ver cómo hallar la solución a las ecuaciones lineales con tres incógnitas:
Como puedes ver, se trata de «anular» el valor de «X» para poder ir sabiendo al valor, primero de z, y luego de y. Cuando tengamos los valores de esas dos incógnitas, nos será muy sencillo sustituirlas por su valor y hallar el valor de X.
¡Hay Ecuaciones hasta con cuatro incógnitas!
En el mundo de las matemáticas siempre hay un paso más allá, siempre se pueden resolver operaciones más complicadas. En este artículo hemos visto cómo despejar x en una ecuación de primer grado, pero también hemos visto cómo resolver correctamente una ecuación de segundo grado y una ecuación lineal con tres incógnitas. Ahora vamos un poco más allá, con un «tutorial» ya más indicado para alumnos que estén en cursos más avanzados, en Bachillerato. Se trata de resolver ecuaciones con 4 incógnitas.
Como también sería bastante difícil explicarlo mediante texto, os dejamos un vídeo en el que podéis ir viendo paso a paso cómo resolver correctamente una ecuación con cuatro incógnitas. Si haces el bachiller de ciencias seguro que nos lo vas a agradecer:
Otros artículos de interés en Espaciociencia:
En Espaciociencia tenemos muchos otros artículos que te pueden resultar muy interesantes: