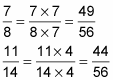Cuando desea restar fracciones con diferentes denominadores, tiene una selección de métodos: la forma fácil, el truco rápido y la forma tradicional. La manera fácil siempre funciona.
Resta fracciones con el método fácil

Esta forma de restar fracciones funciona en todos los casos y es fácil. Aquí está la manera fácil de restar fracciones que tienen diferentes denominadores:
-
Multiplica en cruz las dos fracciones y resta el segundo número del primero para obtener el numerador de la respuesta. Por ejemplo, suponga que desea restar 6/7 – 2/5. Para obtener el numerador, multiplique en forma cruzada las dos fracciones y luego reste el segundo número del primer número:

(6 5) – (2 7) = 30 – 14 = 16
Después de hacer una multiplicación cruzada, asegúrate de restar en el orden correcto. (El primer número es el numerador de la primera fracción por el denominador de la segunda).
-
Multiplica los dos denominadores para obtener el denominador de la respuesta.
7 5 = 35
-
Poner el numerador sobre el denominador te da tu respuesta.

Aquí hay otro ejemplo para trabajar:
Este ejemplo pone todos los pasos juntos:
Con el problema planteado así, solo tienes que simplificar el resultado:
En este caso, puedes reducir la fracción:
Resta fracciones con el método del truco rápido
La forma fácil funciona mejor cuando los numeradores y los denominadores son pequeños. Cuando sean más grandes, es posible que puedas tomar un atajo.

Antes de restar fracciones con diferentes denominadores, verifica los denominadores para ver si uno es múltiplo del otro. Si es así, puedes usar el truco rápido:
-
Aumenta los términos de la fracción con el denominador más pequeño para que tenga el denominador más grande.
Por ejemplo, suponga que desea encontrar 17/20 – 31/80. Si multiplica de forma cruzada estas fracciones, sus resultados serán mucho más grandes de lo que desea trabajar. Pero, afortunadamente, 80 es un múltiplo de 20, por lo que puedes usar la forma rápida.
Primero, aumenta los términos de 17/20 para que el denominador sea 80:

So = 80 ÷ 20 17 = 68

-
Vuelva a escribir el problema, sustituyendo esta versión aumentada de la fracción, y reste.
Aquí está el problema como una resta de fracciones con el mismo denominador, que es mucho más fácil de resolver:

En este caso, no tienes que reducir a los términos más bajos, aunque en otros problemas puede que tengas que hacerlo.
Resta fracciones con el método tradicional
Debe usar la forma tradicional solo como último recurso, cuando el numerador y el denominador son demasiado grandes para usar la forma fácil y cuando no puede usar el truco rápido. Para usar la forma tradicional de restar fracciones con dos denominadores diferentes, sigue estos pasos:
-
Encuentra el mínimo común múltiplo (MCM) de los dos denominadores.
Por ejemplo, suponga que desea restar 7/8 – 11/14. Aquí se explica cómo encontrar el MCM de 8 y 14 usando el método de descomposición en factores primos:
8 = 2 2 2
14 = 2 7
En este ejemplo, se subraya el caso en el que cada factor primo aparece con mayor frecuencia: 2 aparece tres veces y 7 aparece una vez. Entonces el MCM de 8 y 14 es:
2 2 2 7 = 56
-
Aumenta cada fracción a términos más altos para que el denominador de cada uno sea igual al MCM.
Los denominadores de ambos deben ser 56:

-
Sustituye estas dos nuevas fracciones por las originales y resta.

Esta vez, no necesitas reducir, porque 5 es un número primo y 56 no es divisible por 5. Sin embargo, en algunos casos, tienes que reducir la respuesta a los términos más bajos.

Una serie de ejercicios sencillos y básicos, para que los mas pequeños pueden ir aprendido.
 Y aquí tienes la posibilidad de ver y hacer mas operaciones:
Y aquí tienes la posibilidad de ver y hacer mas operaciones: